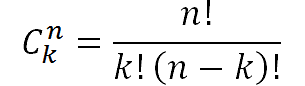miércoles, 22 de marzo de 2017
domingo, 12 de marzo de 2017
domingo, 5 de marzo de 2017
UNIDAD 2. PRINCIPIOS BÁSICOS DE LA PROBABILIDAD
INTRODUCCIÓN
El termino de probabilidad mide la mayor o menor posibilidad de que se de un determinado resultado (suceso o evento) cuando se realiza un experimento aleatorio. Para calcular la posibilidad de un evento se toma en cuenta todos los casos posibles de ocurrencia del mismo es decir, de cuantas formas puede ocurrir determinada situación.
Los casos favorables de ocurrencia de un evento serán que cumplan con la condición que estamos buscando.
En esta investigación se introducen los principios básicos de la probabilidad que nos ayudan a probar las probabilidades de un dicho problema llegando a un posible resultado.
¿QUE ES LA PROBABILIDAD?
Es la rama de las matemáticas que se ocupa de medir o determinar cuantitativamente la posibilidad de que ocurra un determinado suceso. Surge con el estudio de los juegos de azar, pero se extiende a todos los fenómenos aleatorios.
Mide la frecuencia con que se obtiene un resultado bajo condiciones suficientemente estables.
¿QUE NOS INDICA LA PROBABILIDAD?
El calculo matemático de probabilidades se basa en situaciones teóricas en las cuales puede configurarse un espacio muestral cuyos sucesos elementales tengan todos la misma probabilidad. La probabilidad de un resultado se representa con un numero entre 0 y 1: el resultado 0 indica que el resultado no ocurrirá nunca y la probabilidad 1 que el resultado ocurrirá siempre.
MODELOS DE PROBABILIDAD
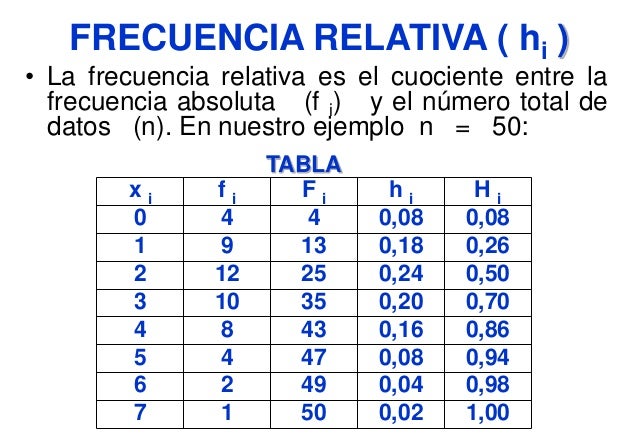
- Frecuencia relativa: Utiliza la observación de datos, registrando su frecuencia de ocurrencia y usando están información para pronosticar la posibilidad de una nueva ocurrencia.
- Frecuencia subjetiva o intuitiva: Se basa en la mejor conjutura con base a la evidencia disponible. Se aplica en eventos nuevos. Es grado de creencia por parte de un individuo de que un evento ocurra, basado en toda la evidencia a su disposición.
- Ejemplo: Si esta nublado, es probable que llueva.
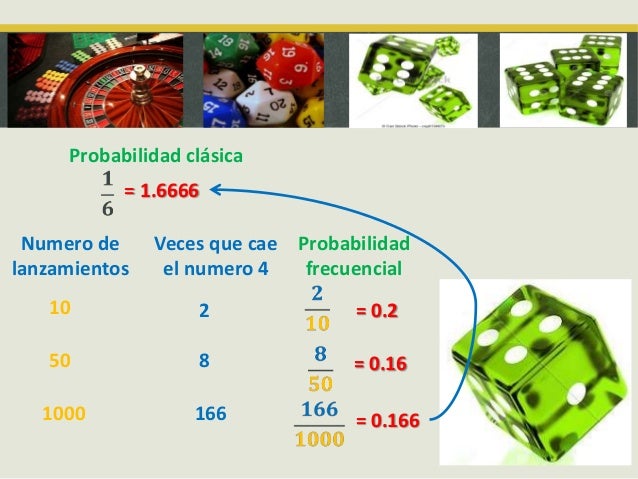
- Frecuencia clásica, a priori o de Laplace: Sirve para determinar la probabilidad de un hecho antes de que ocurra, mediante el calculo teórico, con base a resultados igualmente probables.
- Frecuencia clásica, a priori o de Laplace: Sirve para determinar la probabilidad de un hecho antes de que ocurra, mediante el calculo teórico, con base a resultados igualmente probables.
ESPACIO MUESTRAL
El conjunto de todos los resultados posibles diferentes de un determinado experimento aleatorio se denomina Espacio Muestral asociado a dicho experimento y se suele representar por Ω. A los elementos de Ω se les denomina sucesos elementales.
Así por ejemplo, el espacio muestral asociado al experimento aleatorio consistente en el lanzamiento de una moneda es Ω= {Cara, Cruz}; el espacio muestral asociado al lanzamiento de un dado es Ω={1, 2, 3, 4, 5, 6}, siendo Cara y Cruz los sucesos elementales asociados al primer experimento aleatorio y 1, 2, 3, 4, 5 y 6 los seis sucesos elementales del segundo experimento aleatorio.
A pesar de la interpretación que tiene el espacio muestral, no es más que un conjunto abstracto de puntos (los sucesos elementales), por lo que el lenguaje, los conceptos y propiedades de la teoría de conjuntos constituyen un contexto natural en el que desarrollar el Cálculo de Probabilidades.
EVENTO
Un evento es el resultado posible o un grupo de resultados posibles de un experimento y es la mínima unidad de análisis para efectos de cálculos probabiliasticos.
TIPOS DE EVENTOS
- ELEMENTAL: A cada elemento o resultado posible del espacio muestral, se le conoce el nombre de evento elemental.
- IMPOSIBLE: Algunos eventos nunca pueden ocurrir en el experimento aleatorio, y por eso se llama imposible.
- SEGURO: Los eventos que siempre suceden en el experimento aleatorio, son llamados eventos seguros.
- COMPLEMENTARIO: Cuando se considera un evento A, el evento que contiene todos los eventos elementales del espacio muestral que no estén en A se denominara elemento complementaria.
TÉCNICAS DE ESTUDIO
Cuando el número de posibles resultados de un experimento es finito, su
espacio muestral es finito y su cardinal es un número natural. Si el experimento
es simple, el espacio muestral es unidimensional, constituido por puntos
muestrales con una sola componente, y el cardinal es simplemente el número
de posibles resultados del experimento, los que se pueden enumerar fácilmente.
Pero si el experimento es combinado, el cardinal puede ser tan grande, que
sería del todo absurdo pretender enumerarlos todos, por ser un proceso lento,
tedioso, costoso y susceptible de errores. Y realmente no es importante poder
enumerarlos, sino saber contarlos.
PRINCIPIO DE CONTEO MULTIPLICATIVO
Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de;
N1 x N2 x ..........x Nr maneras o formas
El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro.
PRINCIPIO DE CONTEO ADITIVO
Dado que la probabilidad se refiere a la potencialidad de ocurrencia de un evento, el principio aditivo se refiere a las formas que ese evento puede ser realizado. Por ejemplo, una persona que define viajar desde Santiago al Litoral Central puede hacerlo por Línea de Buses A, Línea de Buses B, Línea de Buses C, Línea de Buses D. El principio aditivo, sería que cada línea de buses representa una alternativa:
L A= 1 ; L B = 1 ; L C = 1 ; L D = 1, (significa que cada línea de buses tiene una línea disponible al litoral central)
En el principio Aditivo sería, que la forma de llegar al punto L sería:
L = 1 + 1 + 1 + 1 = 4
La clave en el principio aditivo es buscar intrínsecamente la “0”, en el ejemplo, la persona para dirigirse al litoral central no puede utilizar todas las alternativas, tiene que utilizar una “o” la otra. Cuando se use el “o”, entonces hay que utilizar el principio aditivo.
COMBINACIÓN
Es todo arreglo de elementos en donde NO nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo, simplemente nos interesa formar grupos y su contenido.
Formula:
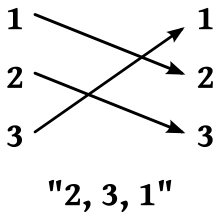
PERMUTACION
Es todo arreglo de elementos en donde SI nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
CONCLUSIÓN
En conclusión estos conceptos son importantes tanto en el estudio de la estadística como en la vida cotidiana ya que es importante saber o memorizar alguno de estos conceptos porque en algún momento donde se llegue a laborar se pueden utilizar la probabilidad como algo fundamental.
Cualquiera que sea la profesión en la estemos,la estadística y la probabilidad es importante en su estudio.
BIBLIOGRÁFICA
miércoles, 1 de marzo de 2017
Suscribirse a:
Comentarios (Atom)